Polygonal Chain¶

class PolygonalChain(*native_anchors: Point, plane: PolarPlane, using_geodesic: bool = True, **kwargs)[source]¶

A path of hmanim.poincare.point.Point objects where two consecutive points are connected by the geodesic line segment between them.

Examples

Example: PolygonalChainExample ¶

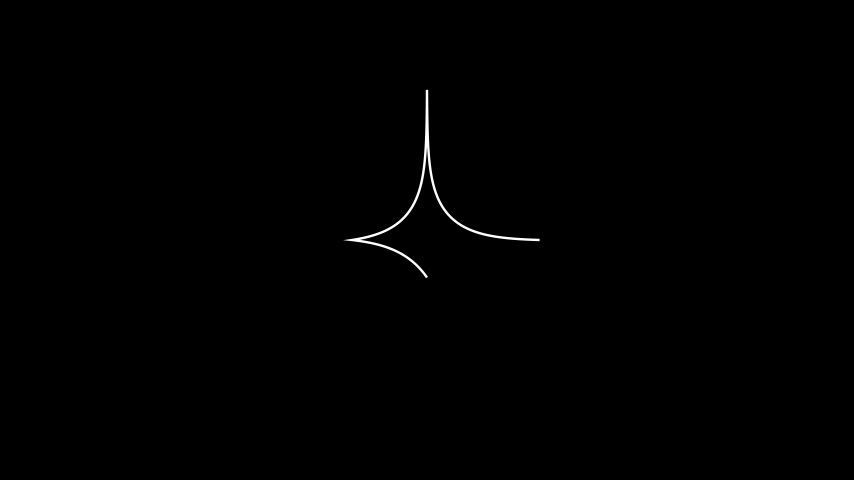
from manim import *

from hmanim.native import Point, PolygonalChain

class PolygonalChainExample(Scene):
    def construct(self):
        # The plane that all our hyperbolic objects live in.
        plane = PolarPlane(size=5)

        # Draw the polygonal chain.
        chain = PolygonalChain(
            *[
                Point(3.0, 0.0),
                Point(4.0, TAU / 4),
                Point(2.0, TAU / 2),
                Point(1.0, TAU * 3 / 4),
            ],
            plane=plane
        )
        self.add(chain)

from hmanim.native import Point, PolygonalChain

class PolygonalChainExample(Scene):
    def construct(self):
        # The plane that all our hyperbolic objects live in.
        plane = PolarPlane(size=5)

        # Draw the polygonal chain.
        chain = PolygonalChain(
            *[
                Point(3.0, 0.0),
                Point(4.0, TAU / 4),
                Point(2.0, TAU / 2),
                Point(1.0, TAU * 3 / 4),
            ],
            plane=plane
        )
        self.add(chain)

copy() → PolygonalChain[source]¶

Create and return an identical copy of the Mobject including all submobjects.

Returns:: The copy.
Return type:: Mobject

Note

The clone is initially not visible in the Scene, even if the original was.

rotated_by(angle: float) → PolygonalChain[source]¶

Rotate the polygonal chain around the origin by a given angle in radians.

Parameters:: angle (float) – The angle to rotate by.
Returns:: The rotated polygonal chain.
Return type:: PolygonalChain

set_center_of_projection(point: Point) → PolygonalChain[source]¶

Set the center of projection of the polygonal chain.

Parameters:: point (hmanim.native.point.Point) – The new center of projection.
Returns:: The polygonal chain with the new center of projection.
Return type:: PolygonalChain

set_curvature(curvature: float) → PolygonalChain[source]¶

Set the curvature of the hyperbolic plane that the polygonal chain lives in.

Parameters:: curvature (float) – The new (negative) curvature.

Note

Affects only the polygonal chain object itself and not the other objects associated with the corresponding hyperbolic plane.

Returns:: The polygonal chain with the new curvature.
Return type:: PolygonalChain

set_native_anchors(native_anchors: Sequence[Point])[source]¶

Change the corner hmanim.poincare.point.Point objects that make up the polygonal chain.

Parameters:: native_anchors (Sequence[hmanim.native.point.Point]) – The new corners.

translated_by(distance: float) → PolygonalChain[source]¶

Translate the polygonal chain by a given distance. See Point.translated_by() for more details.

Parameters:: distance (float) – The distance to translate by.
Returns:: The translated polygonal chain.
Return type:: PolygonalChain

class PolygonalChainRotate(mobject=None, *args, use_override=True, **kwargs)[source]¶

Rotate a polygonal chain around the origin by a given angle.

Examples

Example: PolygonalChainRotateExample ¶

from manim import *

from hmanim.native import Point, PolygonalChain, PolygonalChainRotate

class PolygonalChainRotateExample(Scene):
    def construct(self):
        # The plane that all our hyperbolic objects live in.
        plane = PolarPlane(size=5)

        # Draw the polygon.
        chain = PolygonalChain(
            *[
                Point(3.0, 0.0),
                Point(4.0, TAU / 4),
                Point(2.0, TAU / 2),
                Point(1.0, TAU * 3 / 4),
            ],
            plane=plane
        )
        self.add(chain)

        # Translate the circle
        self.play(
            PolygonalChainRotate(
                chain,
                angle=TAU / 4,
            )
        )

from hmanim.native import Point, PolygonalChain, PolygonalChainRotate

class PolygonalChainRotateExample(Scene):
    def construct(self):
        # The plane that all our hyperbolic objects live in.
        plane = PolarPlane(size=5)

        # Draw the polygon.
        chain = PolygonalChain(
            *[
                Point(3.0, 0.0),
                Point(4.0, TAU / 4),
                Point(2.0, TAU / 2),
                Point(1.0, TAU * 3 / 4),
            ],
            plane=plane
        )
        self.add(chain)

        # Translate the circle
        self.play(
            PolygonalChainRotate(
                chain,
                angle=TAU / 4,
            )
        )

interpolate_mobject(alpha: float)[source]¶

Interpolates the mobject of the Animation based on alpha value.

Parameters:: alpha – A float between 0 and 1 expressing the ratio to which the animation is completed. For example, alpha-values of 0, 0.5, and 1 correspond to the animation being completed 0%, 50%, and 100%, respectively.

class PolygonalChainTranslate(mobject=None, *args, use_override=True, **kwargs)[source]¶

Translate a polygonal chain horizontally by a given distance.

Examples

Example: PolygonalChainTranslateExample ¶

from manim import *

from hmanim.native import Point, PolygonalChain, PolygonalChainTranslate

class PolygonalChainTranslateExample(Scene):
    def construct(self):
        # The plane that all our hyperbolic objects live in.
        plane = PolarPlane(size=5)

        # Draw the polygonal chain.
        chain = PolygonalChain(
            *[
                Point(3.0, 0.0),
                Point(4.0, TAU / 4),
                Point(2.0, TAU / 2),
                Point(1.0, TAU * 3 / 4),
            ],
            plane=plane
        )
        self.add(chain)

        # Translate the polygonal chain.
        self.play(
            PolygonalChainTranslate(
                chain,
                distance=3
            )
        )

from hmanim.native import Point, PolygonalChain, PolygonalChainTranslate

class PolygonalChainTranslateExample(Scene):
    def construct(self):
        # The plane that all our hyperbolic objects live in.
        plane = PolarPlane(size=5)

        # Draw the polygonal chain.
        chain = PolygonalChain(
            *[
                Point(3.0, 0.0),
                Point(4.0, TAU / 4),
                Point(2.0, TAU / 2),
                Point(1.0, TAU * 3 / 4),
            ],
            plane=plane
        )
        self.add(chain)

        # Translate the polygonal chain.
        self.play(
            PolygonalChainTranslate(
                chain,
                distance=3
            )
        )

interpolate_mobject(alpha: float)[source]¶

Interpolates the mobject of the Animation based on alpha value.

Parameters:: alpha – A float between 0 and 1 expressing the ratio to which the animation is completed. For example, alpha-values of 0, 0.5, and 1 correspond to the animation being completed 0%, 50%, and 100%, respectively.