Disk

class Disk(radius: float | None = None, color: ParsableManimColor = ManimColor('#FC6255'), **kwargs: Any)

The Poincaré disk in which other hyperbolic objects live.

Examples

Example: DiskExample

from manim import *

from hmanim.poincare import Disk, Point

class DiskExample(Scene):
    def construct(self):
        disk = Disk(
            radius=3,
            color=WHITE,
        )
        self.add(disk)

from hmanim.poincare import Disk, Point

class DiskExample(Scene):
    def construct(self):
        disk = Disk(
            radius=3,
            color=WHITE,
        )
        self.add(disk)

static circle_intersect(c0: ndarray, r0: float, c1: ndarray, r1: float) → tuple[ndarray, ndarray] | None

Finds the intersection of two circles.

Parameters:

• c0 (np.ndarray) – The center of the first circle.

• r0 (float) – The radius of the first circle.

• c1 (np.ndarray) – The center of the second circle.

• r1 (float) – The radius of the second circle.

Returns:

The coordinates of the intersection points. If there are no intersection points, then None is returned.

Return type:

tuple[np.ndarray, np.ndarray] | None

Examples

Example: CircleIntersectionExample

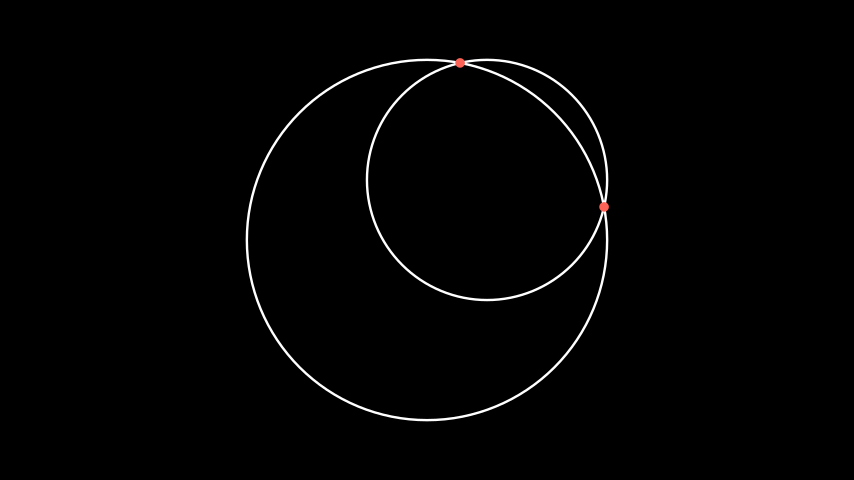
from manim import *

from hmanim.poincare import Disk, Point

class CircleIntersectionExample(Scene):
    def construct(self):
        circle1 = Circle(radius=3, color=WHITE)
        circle2 = Circle(radius=2, color=WHITE).move_to(np.array([1, 1, 0]))
        self.add(circle1, circle2)

        intersections = Disk.circle_intersect(
            circle1.get_center(),
            circle1.radius,
            circle2.get_center(),
            circle2.radius,
        )

        if intersections is not None:
            self.add(
                Dot(intersections[0], color=RED),
                Dot(intersections[1], color=RED),
            )

from hmanim.poincare import Disk, Point

class CircleIntersectionExample(Scene):
    def construct(self):
        circle1 = Circle(radius=3, color=WHITE)
        circle2 = Circle(radius=2, color=WHITE).move_to(np.array([1, 1, 0]))
        self.add(circle1, circle2)

        intersections = Disk.circle_intersect(
            circle1.get_center(),
            circle1.radius,
            circle2.get_center(),
            circle2.radius,
        )

        if intersections is not None:
            self.add(
                Dot(intersections[0], color=RED),
                Dot(intersections[1], color=RED),
            )

coordinates_of_geodesic_circle_through(p1: Point | IdealPoint, p2: Point | IdealPoint) → tuple[ndarray, float, bool] | None

Determines the coordinates of the circle that passes through the (potentially ideal) points p1 and p2. The part of the corresponding circle that lies in the inside of the disk represents the geodesic line segment between the two points.

Parameters:

• p1 (hmanim.poincare.point.Point | IdealPoint) – The first point.

• p2 (hmanim.poincare.point.Point | IdealPoint) – The second point.

Returns:

The coordinates of the center of the circle, the radius of the circle, and a boolean indicating whether the circle center lies within the disk.

Return type:

tuple[np.ndarray, float, bool] | None

Examples

Example: GeodesicCircleExample

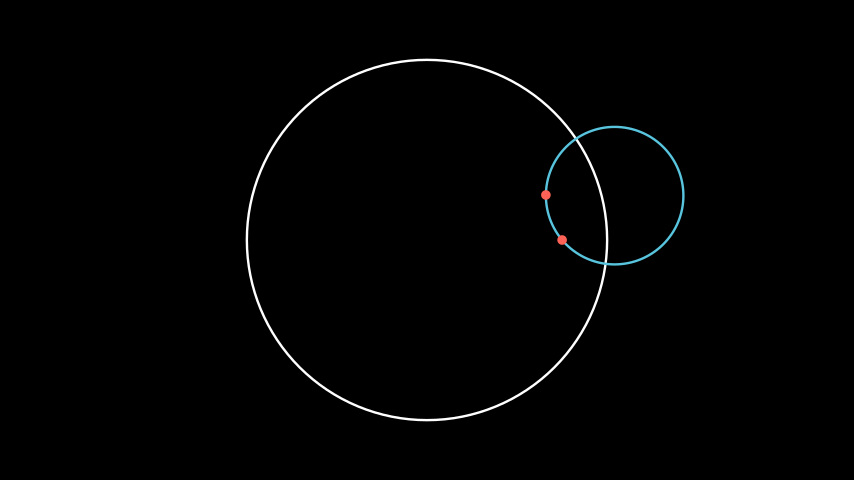
from manim import *

from hmanim.poincare import Disk, Dot, Point

class GeodesicCircleExample(Scene):
    def construct(self):
        disk = Disk(
            radius=3,
            color=WHITE,
        )
        self.add(disk)

        p1 = Point(0.75, 0.0)
        p2 = Point(0.66, 0.25)

        center, radius, in_disk = disk.coordinates_of_geodesic_circle_through(
            p1, p2
        )

        circle = Circle(
            radius=radius,
            color=BLUE,
        ).move_to(center)

        self.add(
            circle,
            Dot(
                p1,
                disk=disk,
                color=RED,
            ),
            Dot(
                p2,
                disk=disk,
                color=RED,
            ),
        )

from hmanim.poincare import Disk, Dot, Point

class GeodesicCircleExample(Scene):
    def construct(self):
        disk = Disk(
            radius=3,
            color=WHITE,
        )
        self.add(disk)

        p1 = Point(0.75, 0.0)
        p2 = Point(0.66, 0.25)

        center, radius, in_disk = disk.coordinates_of_geodesic_circle_through(
            p1, p2
        )

        circle = Circle(
            radius=radius,
            color=BLUE,
        ).move_to(center)

        self.add(
            circle,
            Dot(
                p1,
                disk=disk,
                color=RED,
            ),
            Dot(
                p2,
                disk=disk,
                color=RED,
            ),
        )

coordinates_of_geodesic_circle_through_ideal(p1: IdealPoint, p2: IdealPoint) → tuple[ndarray, float, bool] | None

Determines the coordinates of the circle that passes through the ideal points p1 and p2. The part of the corresponding circle that lies in the inside of the disk represents the geodesic line between the two points.

Parameters:

• p1 (IdealPoint) – The first ideal point.

• p2 (IdealPoint) – The second ideal point.

Returns:

The coordinates of the center of the circle, the radius of the circle, and a boolean indicating whether the circle center lies within the disk.

Return type:

tuple[np.ndarray, float, bool] | None

Examples

Example: IdealGeodesicCircleExample

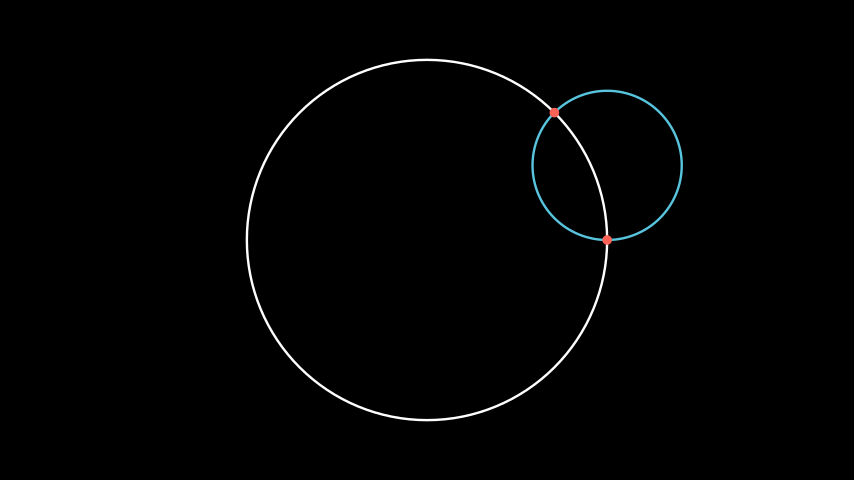
from manim import *

from hmanim.poincare import Disk, Dot, IdealPoint

class IdealGeodesicCircleExample(Scene):
    def construct(self):
        disk = Disk(
            radius=3,
            color=WHITE,
        )
        self.add(disk)

        p1 = IdealPoint(angle=0)
        p2 = IdealPoint(angle=TAU / 8)

        center, radius, in_disk = disk.coordinates_of_geodesic_circle_through_ideal(
            p1, p2
        )

        circle = Circle(
            radius=radius,
            color=BLUE,
        ).move_to(center)

        self.add(
            circle,
            Dot(
                p1,
                disk=disk,
                color=RED,
            ),
            Dot(
                p2,
                disk=disk,
                color=RED,
            ),
        )

from hmanim.poincare import Disk, Dot, IdealPoint

class IdealGeodesicCircleExample(Scene):
    def construct(self):
        disk = Disk(
            radius=3,
            color=WHITE,
        )
        self.add(disk)

        p1 = IdealPoint(angle=0)
        p2 = IdealPoint(angle=TAU / 8)

        center, radius, in_disk = disk.coordinates_of_geodesic_circle_through_ideal(
            p1, p2
        )

        circle = Circle(
            radius=radius,
            color=BLUE,
        ).move_to(center)

        self.add(
            circle,
            Dot(
                p1,
                disk=disk,
                color=RED,
            ),
            Dot(
                p2,
                disk=disk,
                color=RED,
            ),
        )

point_by_inverting(p: Point) → Point

Invert a class:hmanim.poincare.point.Point in the disk.

Note

For more information on the inversion, see https://en.wikipedia.org/wiki/Inversive_geometry#Inversion_in_a_circle.

Parameters

point (hmanim.poincare.point.Point): The point to invert.

Returns

The inverted point.

Examples

Example: DiskPointInversionExample

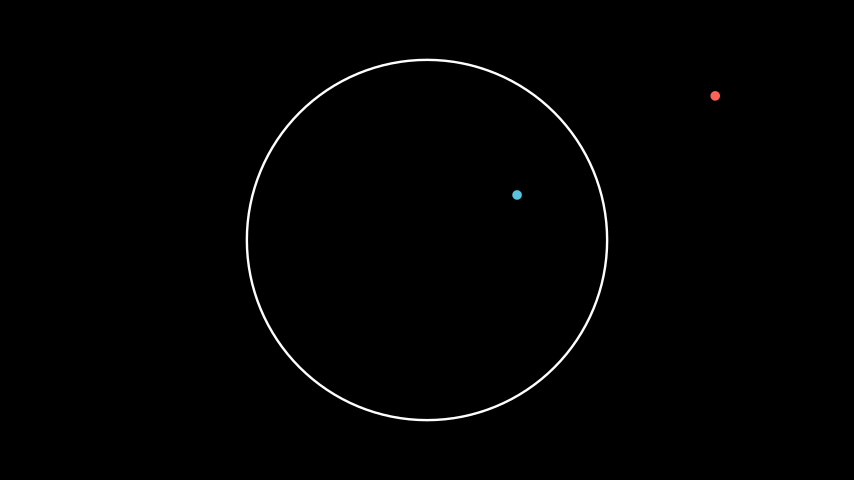
from manim import *

from hmanim.poincare import Disk, Dot, Point

class DiskPointInversionExample(Scene):
    def construct(self):
        disk = Disk(radius=3, color=WHITE)
        self.add(disk)

        point = Point(0.5, 0.25)
        inverted = disk.point_by_inverting(point)
        self.add(
            Dot(
                point,
                disk=disk,
                color=BLUE,
            ),
            Dot(
                inverted,
                disk=disk,
                color=RED,
            ),
        )

from hmanim.poincare import Disk, Dot, Point

class DiskPointInversionExample(Scene):
    def construct(self):
        disk = Disk(radius=3, color=WHITE)
        self.add(disk)

        point = Point(0.5, 0.25)
        inverted = disk.point_by_inverting(point)
        self.add(
            Dot(
                point,
                disk=disk,
                color=BLUE,
            ),
            Dot(
                inverted,
                disk=disk,
                color=RED,
            ),
        )

point_from_scaled(coordinates: Sequence[float]) → Point

The inverse of the scaled_point() method. Converts a point from the canvas to the unit disk.

Parameters:

• coordinates (Sequence[float]) – The coordinates of the point which we

• disk. (want to convert back to a point within the unit)

Returns:

The point within the unit disk.

Return type:

hmanim.poincare.point.Point

scaled_point(p: Point) → ndarray

Used to convert a point from within unit disk (as is used to represent the Poincaré disk) to the scaled version that we use for drawing. Essentially, this allows us to draw the Poincaré (unit) disk as a disk of arbitrary radius on the canvas.

Parameters:

p (hmanim.poincare.point.Point) – The point to scale.

Returns:

The coordinates of the scaled point.

Return type:

np.ndarray